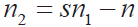低能电子对单面介质加载微波部件微放电的影响*
编者按:在微波设备微放电效应的研究中,低能电子的作用通常被忽略。本文重点研究了低能电子对单面介质加载微波部件微放电的影响,基于蒙特卡洛算法,建立了单面介质加载微波部件的微放电的模型,模拟了单面介质加载微波部件微放电的规律,利用数值的方法对波导中静电场进行求解并对电子的轨迹进行跟踪。通过对比经典的Vaughan二次电子发射模型(考虑低能电子)和Rice模型(没有考虑低能电子)的模拟结果,获得了低能电子对单面介质加载微波部件微放电的影响。
*基金项目:湖南省自然科学基金(2017JJ3314)
0 引言
微放电效应(也被称为二次电子倍增效应)是在真空条件下运行在微波和毫米波子系统中,在微波设备和微波元件中经常能观察到的一种高功率共振电子放电,存在于各种不同的高功率微波场景中,如卫星通信有效载荷的无源部件、行波管、高功率射频窗口以及粒子加速器等[1]。
在许多现代射频系统中,二次电子倍增效应是在真空或接近真空条件下工作的一个重要失效机制[2]。这种现象表现为自由电子在真空器件内的雪崩式增长,这是在射频电场的作用下,被加速的高能电子撞击器件表面时,从器件表面激发出新的二次电子发射引起的。在不同的射频系统中,如星载通信、射频加速器和高功率微波发生器,二次电子倍增击穿问题变得越来越严重,这是为了满足高性能的需求,微波功率不断增加,并且尽可能减小制造微波装置的尺寸所导致的。由于二次电子倍增放电可以显著限制甚至损坏射频系统,所以研究射频系统中的二次电子倍增放电,对减少射频系统的损坏有至关重要的作用[3-6]。这项工作将对快速发展的二次电子倍增效应的研究做出重大贡献,将使研究人员能够更好地设计射频系统,同时,也使得二次电子倍增效应成为了空间研究领域重点关注的热点课题之一[7]。在过去几十年中,存在于金属表面和介质表面之间的二次电子倍增效应已经引起了极大的关注。介质表面的二次电子倍增与金属表面不同,在射频电场的作用下,二次电子不会在金属表面积累电荷,但会在介质表面积累相应的正电荷或负电荷[8],这些积累在介质表面的电荷会形成一个静电场,影响电子的运动[9]。
本文将通过对比经典的Vaughan 模型和Rice 模型在单面介质加载微波部件中二次电子倍增效应的差异,以获得低能电子对单面介质加载微波部件中微放电的影响。
1 模型介绍
图1 展示了在下表面加载了介质的金属平行板波导的示意图,其中金属平行板的长度和间距分别为a 和d。加载的介质层厚度为h,介质表面和金属表面之间的间隙为H = d-h。在模型中设置了余弦变化的射频电场(其中,E0 的取值为2×106 V/m),工作频率为f(对应不同的谐振阶数时,f 的取值有所不同),其对应的仿真时间步长设置为RF 周期的1/1 000,在每个射频周期内电子运动1 000 个时间步,以保证仿真的精确度。设置初始电子的数目为N0 = 1 000,在前500 个时间步内,每个时间步从介质表面发射出2 个初始电子。每个初始电子的权重都设置为1,为了更加高效地进行计算,将电子数目的阈值上限设置为Nth = 1×106。当电子的数目超过Nth 时,会在下一步的模拟中将电子的数目随机减少一半,同时使剩余电子的电荷和质量增加1 倍。在相反的情况下,当电子数目少于Nth 的10% 时,会在下一步的模拟中将每个电子分成2 个电子,并将电子的电荷和质量减半[10]。以这样的方法进行计算,既保证了计算可行性,同时又保证了参与计算的电子数目。当激发出新的二次电子时,等效的正电荷会在介质表面积聚,形成非均匀分布的静电场。随着正电荷的不断积聚,静电场的强度亦随之增强,双面倍增可能演变为单面倍增并自我维持或熄灭,这容易受到许多其他因素的影响。当单面倍增发生时,电子云将在每个整数射频周期内冲击介质表面。
设置材料的最大二次电子产额系数为δmax0 = 2.36,与之对应的入射能量为Wmax0 = 300 eV[11],两种模型的SEY 随入射能量的变化如图2 所示。从图中可知,经典的Vaughan 模型将能量低于12.5 eV 的电子视为无效电子,没有考虑其与金属或介质表面的碰撞,而Rice模型则将其考虑在内并视为弹性散射电子[12]。经典的Vaughan 二次电子发射模型如下所示:
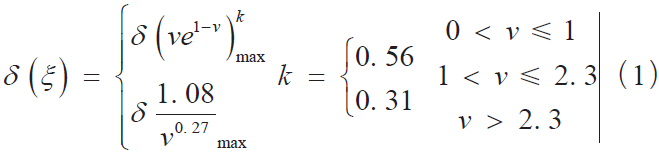
Rice 模型对经典的Vaughan 模型进行了修改,其模型如下所示:
![]()
其中,v = (Wim-Wth) / (Wmax-Wth),参数δmax、Wmax 和Wth 由材料和表面处理所决定。
初始电子从介质表面被随机发射出去,初始电子的发射能量W0 满足Maxwell-Boltzmann 分布,如式(3)所示:

初始电子的发射角度服从正弦分布,如式(4)所示:
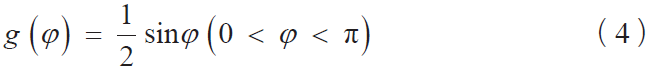
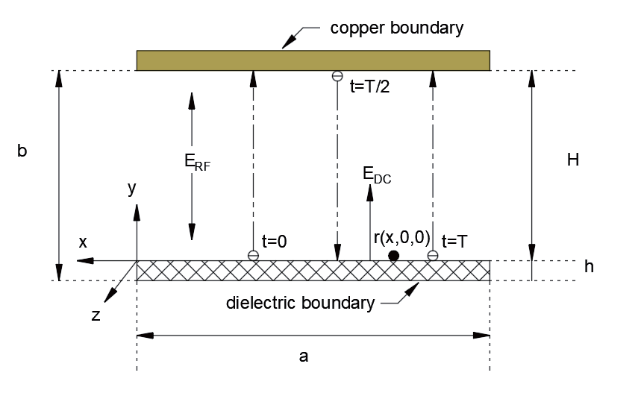
图1 单面介质加载平行板波导模型
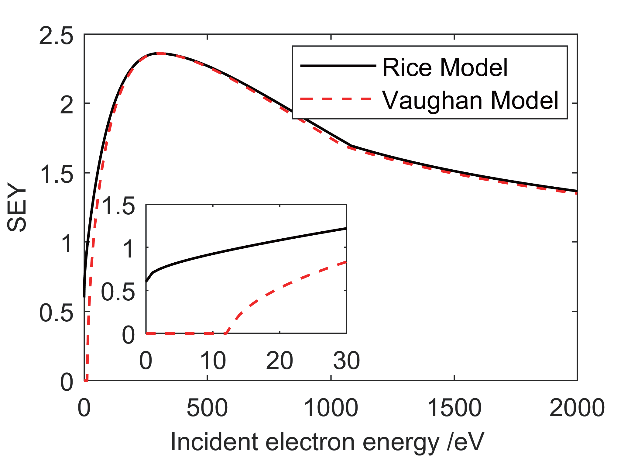
图2 SEY曲线
2 静电场的计算
当电子与介质表面发生碰撞时,会在介质表面积聚电荷,然而电子与金属表面碰撞则不会在金属表面积聚电荷,两者之间存在着差异。当介质表面的电荷积聚到一定数量时,就会形成一个非均匀分布的静电场来影响电子的运动。所以,模型中静电场的精确求解,对后续电子的运动具有重要的影响。本文采用数值的方法对介质表面由电荷积聚所产生的静电场进行求解,设置电荷位于介质表面的r(x,h,0)处,静电场的求解如式(5)所示:
![]()
为了求解模型中静电场的分布,我们应该先对表面电荷积聚所产生的电势求解,利用叠加原理,通过增加每个电荷各自的贡献,就可以得到介质表面的电荷在波导中产生的电势分布,其表达式如下所示:
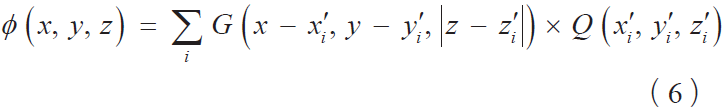
其中,G 为单位电荷形成电势的格林函数,求解出电势的格林函数就能求解得到电势。G的展开如式(7)所示:

为了方便计算,在本文中假设点电荷沉积的位置位于介质表面和真空区域的交界处来进行计算。所考虑问题的几何特征和线性性质使得狄拉克函数的展开可以如式(8)(9)所示:
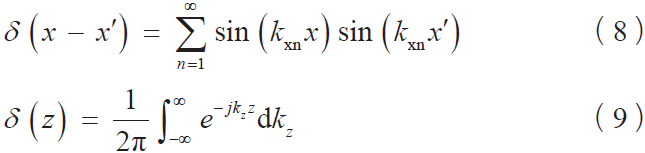
其中,kxn = nπ/a,kz 是沿着z 方向的傅里叶变换。
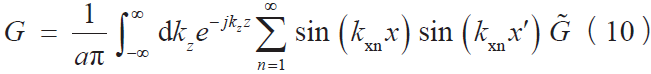
其中,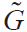 是频域中的格林函数。结合式(7)就可以求解出
是频域中的格林函数。结合式(7)就可以求解出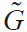 为:
为:
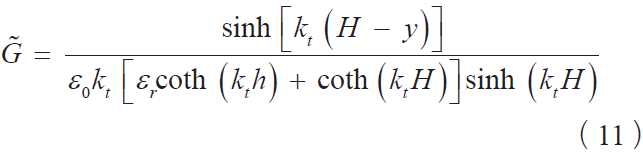
把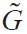 代入到式(5)中,就能求解出介质表面的电荷在模型中的电势分布,从而求解出模型中静电场的空间分布。
代入到式(5)中,就能求解出介质表面的电荷在模型中的电势分布,从而求解出模型中静电场的空间分布。
为了验证所求出的静电场在模型中的分布是否正确,下面在介质表面积聚固定数量的正电荷来进行模拟。令介质表面每个位置都均匀分布了1×107 个正电荷,在模型中产生的静电场分布如图3 所示,图中箭头的方向代表静电场的方向,箭头的长度代表静电场的强度。从图中可以看出,静电场沿着介质表面呈现均匀分布,随着与介质表面之间距离的增加,静电场的强度呈现逐渐减弱的趋势。取x = 5 mm 处的静电场进行分析,静电场的强度随介质表面距离的变化,如图4 所示,此时,静电场最强的位置为介质表面达到了Edc = 1.37×105,在金属表面的静电场的强度最弱。模拟的结果和理论的结果保持一致,验证我们理论的可行性。
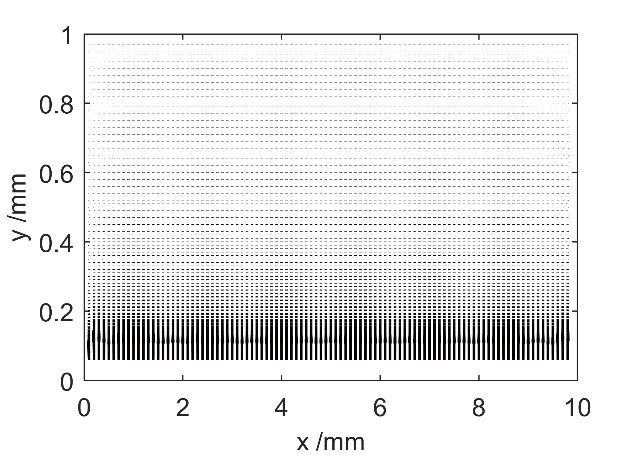
图3 静电场在模型中的分布
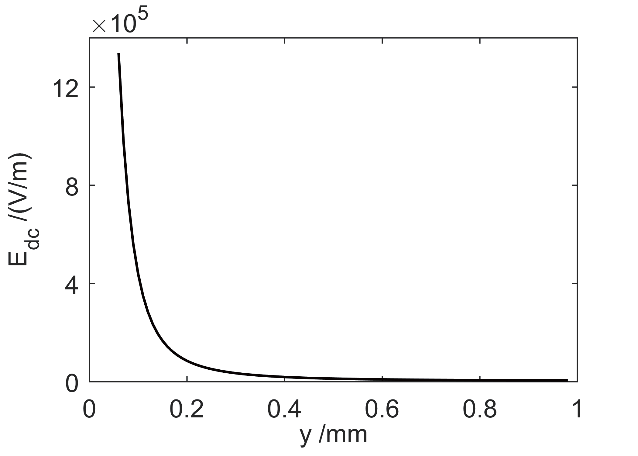
图4 静电场的强度随介质表面距离的变化
3 电子的动力学方程
我们通过忽略RF 磁场简化了模型,可以通过在每个时间步中数值求解洛伦兹方程来计算电子的轨迹。在射频电场ERF 的作用下,电子在金属与介质表面之间周期性地运动,当与介质表面碰撞时,在激发新二次电子的同时会积聚相应的电荷,形成静电场从而影响电子的运动。模型中电子的动力学方程如式(12)~(19)所示:
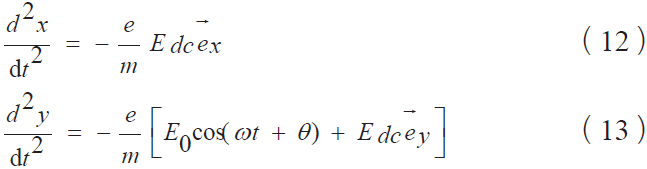
设置初始条件,初始时刻t=0 时的速度为:
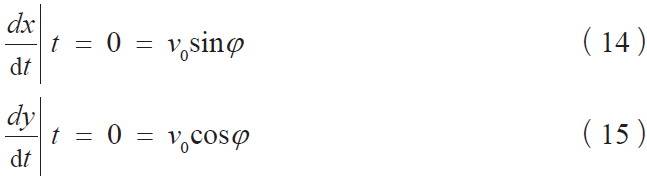
沿着x,y 方向的速度分别为:
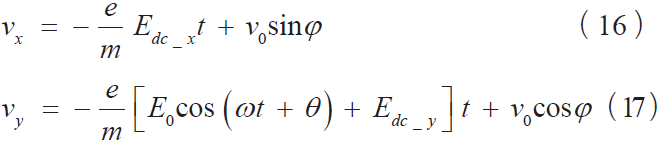
沿着x,y 方向的位移分别为:
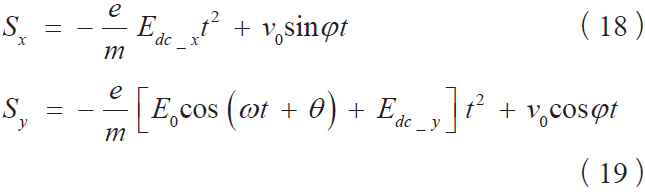
4 实验结果分析
平行板波导模型的长度为a = 10 mm,间隙距离为d = 1 mm,介质层的厚度为h = 0.05 mm。因此,金属与介质表面之间的间距为H = 0.95 mm。设置RF 电压VRF = 1.9 kV,工作频率f = 6 GHz,在该参数下为一阶的谐振阶数。两种模型下,电子数目随时间的变化如图5 所示,通过对比电子数目Ne 随时间的变化可知,Rice 模型的二次电子倍增速率要大于经典的Vaughan模型, 并且在达到短暂的饱和时电子数目达到了Ne_R = 4×108,比经典的Vaughan 模型达到饱和时的电子数目Ne_V = 6×106 要更多, 两种模型在达到短暂饱和之后的趋势也有所不同,Rice 模型在达到饱和之后,Ne_R 仍然以极小的速度继续增长,但是经典的Vaughan 模型在达到饱和之后,Ne_V 呈现下降的趋势。与之对应的静电场Edc 随时间的变化如图6 所示,两种模型在达到饱和之后Edc 都达到了饱和并保持稳定,但Rice 模型达到饱和时的静电场为Edc_R = 4×105,而经典的Vaughan 模型在达到饱和时的静电场为Edc_V = 2.3×105。图7 展示了两种模型在电子数目达到饱和之后,电子相的空间分布。从图7(a)中可以看出,在达到饱和时,经典的Vaughan 模型的电子在波导中呈现均匀分布的状态,而从图7(b)中可知,在达到饱和时,Rice 模型的电子主要分布在波导的介质表面附近,随着与介质表面距离的增加,电子数目呈现减少的趋势。图8 和图9 分别展示了两个模型下平均SEY 和平均电子能量随时间的变化,从图8(a)可知,经典的Vaughan 模型在达到饱和之后平均SEY<1,入射电子大于激发的二次电子,电子数目呈下降趋势,与之对应平均电子能量如图9(a)所示,稳定在Wave = 21 eV,Rice 模型在达到饱和之后平均SEY > 1,入射电子大于激发的二次电子,电子数目呈现缓慢的增长,如图8(b)所示,平均电子能量稳定在Wave = 15 eV,如图9(b)所示。
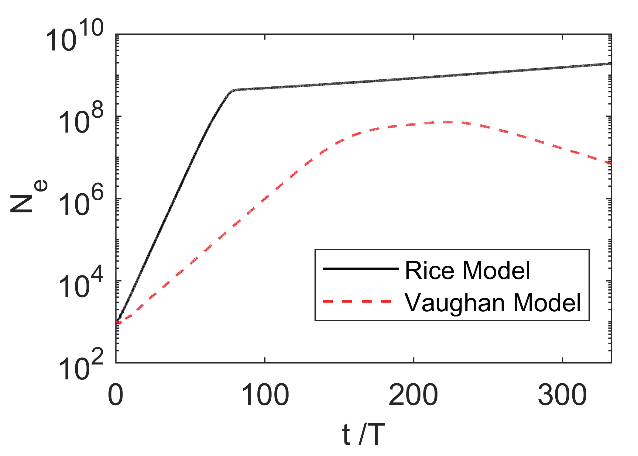
图5 电子数目随时间的变化
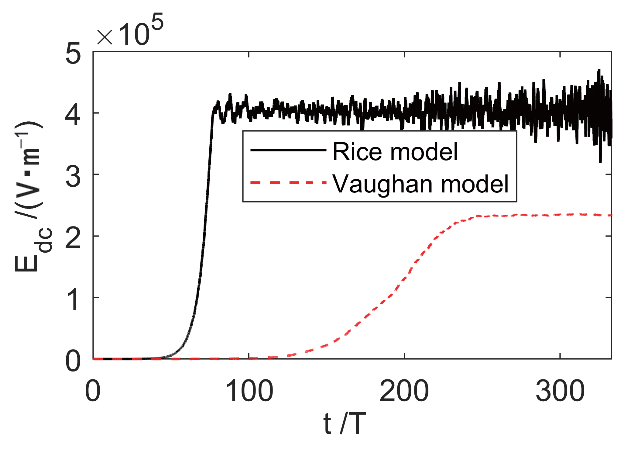
图6 静电场随时间的变化
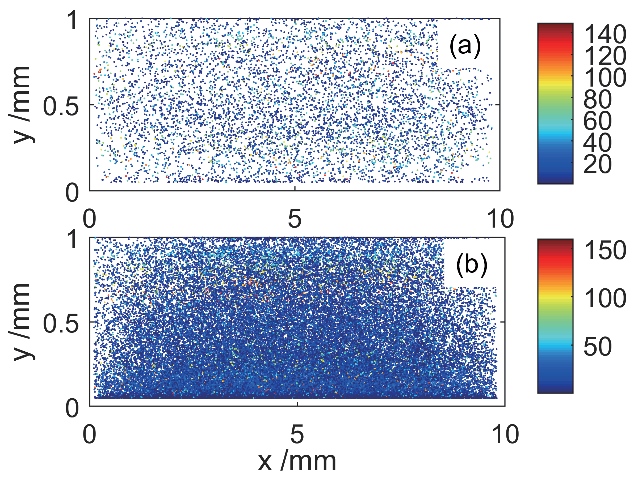
图7 电子的相空间分布,(a)为Vaughan模型,(b)为Rice模型
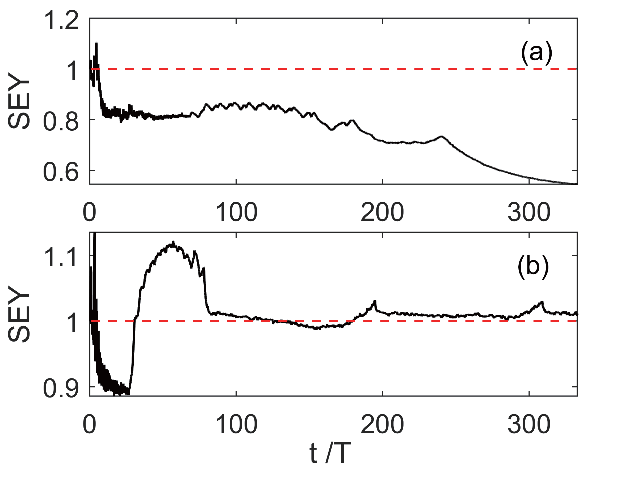
图8 平均SEY随时间的变化,(a)为Vaughan模型,(b)为Rice模型
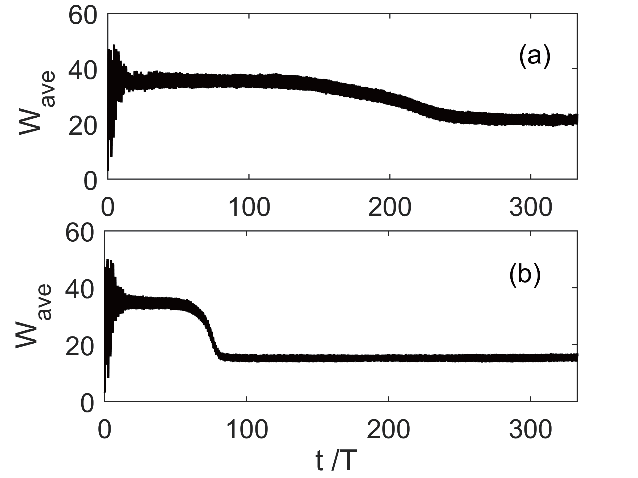
图9 平均电子能量随时间的变化,(a)为Vaughan模型,(b)为Rice模型
4 结束语
本文分别对经典的Vaughan 模型和Rice 模型在单面介质加载微波部件中的微放电效应进行了模拟仿真。研究结果表明,Rice 模型在电子的增长速率、达到饱和时电子的数目和静电场的强度都要高于经典的Vaughan模型,考虑低能电子的二次电子发射模型更适合用于研究微波设备的微放电效应。
参考文献:
[1] 崔万照,李韵,张洪太,等.航天器微波部件微放电分析及其应用[M].北京:人民邮电出版社,2019.
[2] 乐群,殷希梅,黄学翔,等.微波部件微放电效应研究[C].电工理论学术年会,2007.
[3] VAGUE J, MELGAREJO J C,GUGLIELMI M,et al.Multipactor effect characterization of dielectric materials for space applications[j].ieee transactions on microwave theory and techniques,2018(66):3644-3655.
[4] POPOVIC S,UPADHYAY J,MAMMOSSER J,et al.Resonantfrequency discharge in a multi-cell radio frequency cavity[J/OL].Journal of Applied Physics,2014,116(11).173301.https://www.researchgate.net/publication/268448052_Resonant-frequency_discharge_in_a_multi-cell_radio_frequency_cavity
[5] COVES A,TORREGROSA-PENALVA G,VICENTE C,et al.Multipactor discharges in parallel-plate dielectric-loaded waveguides including space-charge effects[J].Electron Devices,IEEE Transactions on,2008,55(9):2505-2511.
[6] TORREGROSA-PENALVA G,COVES A,GIMENO MARTINEZ B,et al.Multipactor susceptibility charts of a parallel-plate dielectric-loaded waveguide[J].IEEE Transactions on Electron Devices,2010,57(5):1160-1166.
[7] 王新波,白鹤,李韵,等.星载微波部件介质微放电理论研究现状及发展趋势[J].空间电子技术,2019(6):1-9.
[8] TORREGROSA G,COVES N,VICENTE C P,et al.Time evolution of an electron discharge in a parallel-plate dielectric-loaded waveguide[J].IEEE Electron Device Letters,2006,27(7):619-621.
[9] BERENGUER,ANDRES,MESA,e t a l.A n a lysis o f mu l t i p a c t o r e f f e c t i n a P a r t i a l l y Di e l e c t r i c - L o a d e d Rectangular Waveguide[J].IEEE Transactions on Plasma Science,2019.
[10] 张雪,王勇,范俊杰,等.金属壁与介质窗之间次级电子倍增效应的研究[J].物理学报,2014,63(16):397-405.
[11] LI Y,WANG D,YU M,et al.Experimental verification of multipactor discharge dynamics between ferrite dielectric and metal[J].IEEE Transactions on Electron Devices,2018(8):1-8.
[12] 张雪,王滔,倪鑫荣,等.低能二次电子对微波输能窗击穿现象的影响[J].强激光与粒子束,2020,32(10).49-54.
(本文来源于《电子产品世界》杂志2021年10月期)

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码