未知负载情况下PWM逆变器的自适应重复控制
2.2 稳定性分析
从图2中我们可以得到: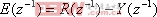 (6)
(6)
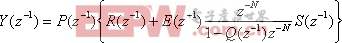 (7)
(7)
从(6)和(7)中消去Y( )便得到:
)便得到:
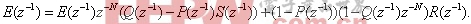 (8)
(8)
图3给出了(8)式的方框图,如果对任意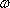 ,如果
,如果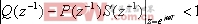 , (9)
, (9)
并且P( )稳定的话,那么e(k)就是有界的,这表明系统是稳定的。对S(
)稳定的话,那么e(k)就是有界的,这表明系统是稳定的。对S( )和Q(
)和Q( )的设计要对
)的设计要对

图3 误差收敛表达式框图
相对稳定性和周期误差的收敛速度进行综合考虑。为简便起见,如果我们选择Q( )为一个略小于1的常数,那么我们就可以选择任意具有很小增益的S(
)为一个略小于1的常数,那么我们就可以选择任意具有很小增益的S( )来满足(9)式的稳定性标准。但即使这样,周期误差可能依然很大。为了同时满足(5)式和(9)式的要求,我们可以在选择一个略小于单位1的常数Q(
)来满足(9)式的稳定性标准。但即使这样,周期误差可能依然很大。为了同时满足(5)式和(9)式的要求,我们可以在选择一个略小于单位1的常数Q( )的同时,选择具有相位超前特性的数字滤波器S(
)的同时,选择具有相位超前特性的数字滤波器S( 4)。当S(
4)。当S( )P(
)P( )拥有接近于零相移的特性时,便可根据相对稳定性和快速收敛速度得到最佳的S(
)拥有接近于零相移的特性时,便可根据相对稳定性和快速收敛速度得到最佳的S( )。
)。
2.3 收敛性分析
在(9)式的稳定性标准中,也可以把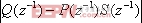 看作是周期误差收敛的性能指标。
看作是周期误差收敛的性能指标。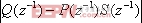 越小,误差收敛速度就越快。收敛系数h的定义为:
越小,误差收敛速度就越快。收敛系数h的定义为:
h =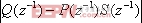 (10)
(10)
果h=0,那么在一个循环之后周期误差将被消除。然而,要满足这一条件需要有P(4)的完美匹配,但这显然是难以实现的。在此,我们定义:
S( ) =
) = 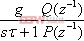 (11)
(11)
其中g是介于0和1之间的常数, 是时常数。
是时常数。
3 自适应重复控制系统
图4为自适应重复控制方案,除传统的重复控制器外,控制环路中还包括自适应参数调谐器。
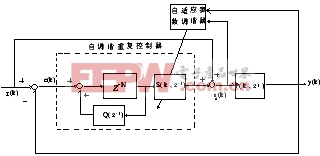
图4 自适应重复控制方案
P(k, )为二次时变系统的转移函数,其表达式为:
)为二次时变系统的转移函数,其表达式为:
P(k, )=
)=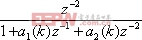 (12)
(12)
式中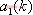 和
和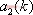 为待定参数。
为待定参数。
从图2中我们可以得到:
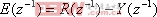
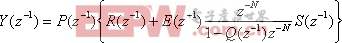
从(6)和(7)中消去Y(

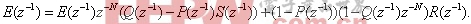
图3给出了(8)式的方框图,如果对任意
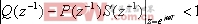
并且P(




相对稳定性和周期误差的收敛速度进行综合考虑。为简便起见,如果我们选择Q(







2.3 收敛性分析
在(9)式的稳定性标准中,也可以把
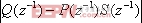
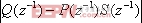
h =
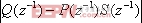
果h=0,那么在一个循环之后周期误差将被消除。然而,要满足这一条件需要有P(4)的完美匹配,但这显然是难以实现的。在此,我们定义:
S(

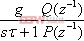
其中g是介于0和1之间的常数,

3 自适应重复控制系统
图4为自适应重复控制方案,除传统的重复控制器外,控制环路中还包括自适应参数调谐器。

P(k,


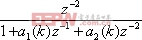
式中
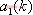

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码