电子产品世界

图6　不同布站半径时的GDOP曲线(z=500m)

　　2.目标速度测量
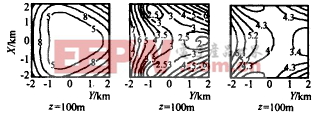
　　(1)目标速度估计期望值　分析图7图8给出的目标速度期望值与高度及布站半径的关系可以看出，由于式(23)的非线性关系，估计目标速度时也会产生偏移量，此偏移量的大小随目标高度的增加而减小.同时当系统布站半径增大时，偏移量先是减小随后又增大.在L=2km时，效果最好.
　　(2)目标速度估计均方根误差　速度估计均方根误差分析结果如图9图10，可以看出，目标越高速度均方根误差越小，而L增大时中心区域的速度均方根误差也增加.

图7　速度期望值与高度的关系(L=2km)

图8　速度期望值与布站半径的关系(z=500m)

图9　速度均方根误差与高度的关系(L=2km)

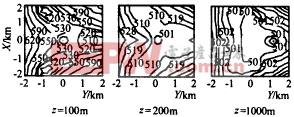
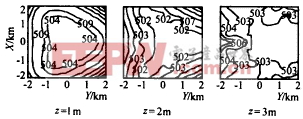
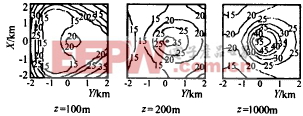
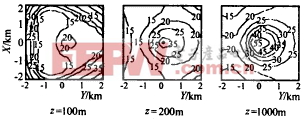
图10　速度均方误差与布站半径的关系(z=500m)

　　(3)定位误差对速度测量的影响　分析表明，高精度定位情况下定位误差对速度测量的影响很小.目标定位误差引起的速度估计偏移量及均方根误差远小于因单站雷达多卜勒测速误差产生的测速偏移量及均方根误差，一般可以忽略.但是，当定位误差增大时，其对速度测量的影响会迅速增大，这时定位误差的影响就不能忽略了.
　　3.细柱状目标长度
　　细柱状目标长度估计的分析结果如图11，12所示，可以看出，z越大偏移量越小，L增大时偏移量先是减小接着又增大，变化关系不是单调的，L=2km时性能最好.目标长度均方根误差与高度及布站半径的关系也有相同的变化规律.

图11　目标长度期望值分布(z=500m)

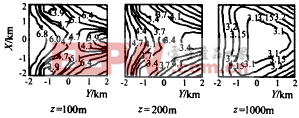
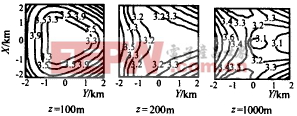
图12　目标长度期望值分布(L=2km)

　　另外，按第六节的方法分析定位误差对目标长度估计的影响，结果表明高精度定位情况下，定位误差对目标长度估计的影响也可以忽略不计.如果不是高精度定位，只需要考虑定位误差的影响.

十、结　　论
　　本文将FMCW波形和单频脉冲波形引入多站雷达系统，在考虑时延和频移解耦，选择合适发射波形的基础上，就近程应用情况下TR-R2系统对目标几何中心定位，目标速度测量及细柱状目标长度估计等问题进行了全面的分析与仿真.得出了一些对工程实践有一定指导意义的结论.特别是文中所讨论的解耦方法具有普遍适用的意义.
　　对系统性能所进行的分析表明，系统性能既与目标位置有关，又与系统布局的几何参数有关.
　　由于存在非线性关系，多站系统在对目标进行定位，测量目标速度及估计目标长度时都会产生偏移量.当目标高度较低时偏移量较大，目标较高时偏移量较小.另外，目标定位误差的GDOP因子，速度以及目标长度估计均方根误差也都随高度的增加而减小.
　　系统布局对性能的影响主要表现为系统布站半径的影响.布站半径越大，定位坐标偏移量越小，目标速度及长度偏移量随布站半径的变化不是单调的，GDOP因子的变化也不是单调的，在本文分析的情况下，L=2km时系统性能最好.
　　高精度定位情况下，定位误差对目标长度及速度测量的影响很小，可以忽略不计.