低Q因子 E类放大器中的谐波抑制
在这篇文章中,我们研究了Q因子不理想的E类功率放大器的滤波要求。
本系列的前一篇文章探讨了E类放大器的理想化操作,并推导出了其设计方程。正如我们在文章末尾讨论的那样,这些方程依赖于负载网络的品质因子(Q)足够高,以确保开关频率下的正弦输出电流。否则,基本设计方程可能无法产生最佳性能所需的零电压和零导数开关条件。
Q的实际范围是3到10,这不足以防止谐波电流流入负载。图1显示了一个基本的E类放大器——为了提供所需的谐波抑制程度,我们需要在其串联谐振电路和负载之间插入一个滤波器。
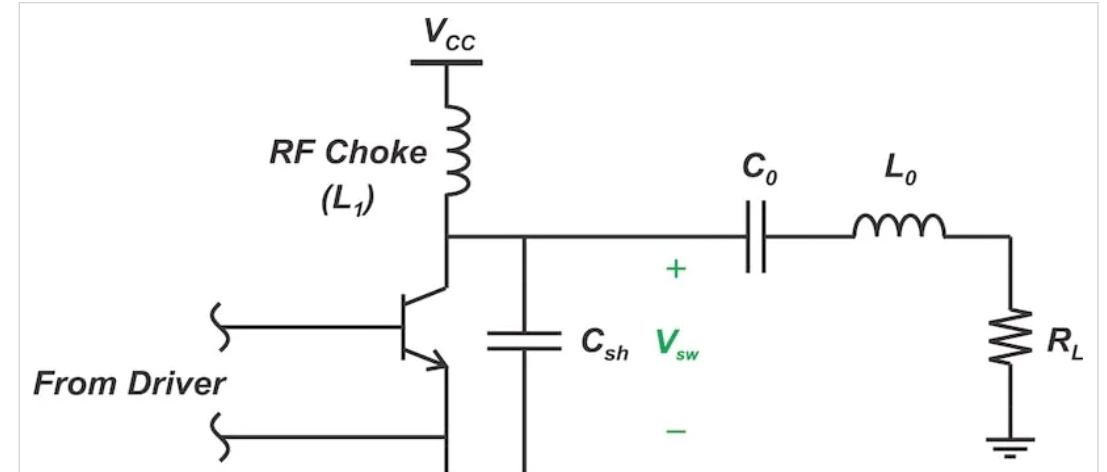
图1 基本E类放大器示意图。图片由Steve Arar提供
在本文中,我们将学习如何确定实现所需谐波抑制所需的滤波器衰减。然而,在我们进行这些计算之前,我们需要讨论放大器开关波形的频率内容。我们从开关电压开始。
开关电压的频率成分
图2显示了E类驱动晶体管的典型开关波形。
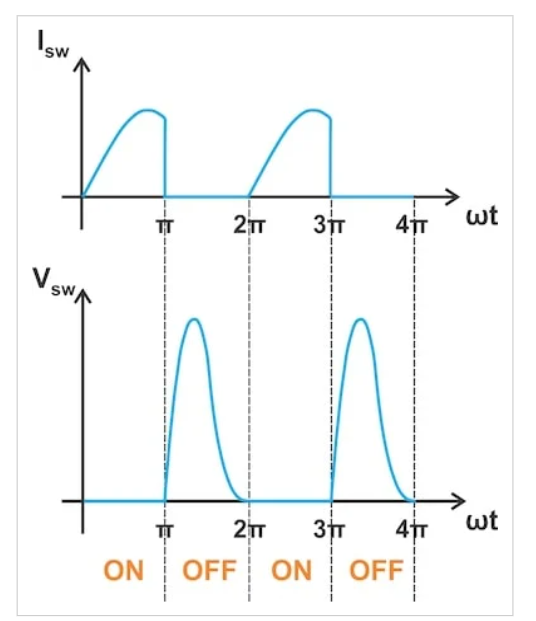
图2 E类放大器中典型的开关电流(顶部)和电压(底部)波形。图片由Steve Arar提供
F.Raab的经典论文“E类调谐功率放大器的理想化操作”计算了开关电压波形的频谱(上图中的Vsw)。在本文中,Raab博士将n次谐波电压分量(Vn)表示为:
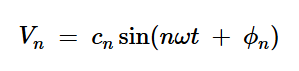
方程式1
解释:
n=谐波数
cn=第n次谐波的振幅
⍵=频率(单位:rad/s)
t=时间
ϕn=第n次谐波的相位角。
他的分析得出了图3所示的光谱。请注意,此图中的cn值已归一化为电源电压。换句话说,它假设Vcc=1。
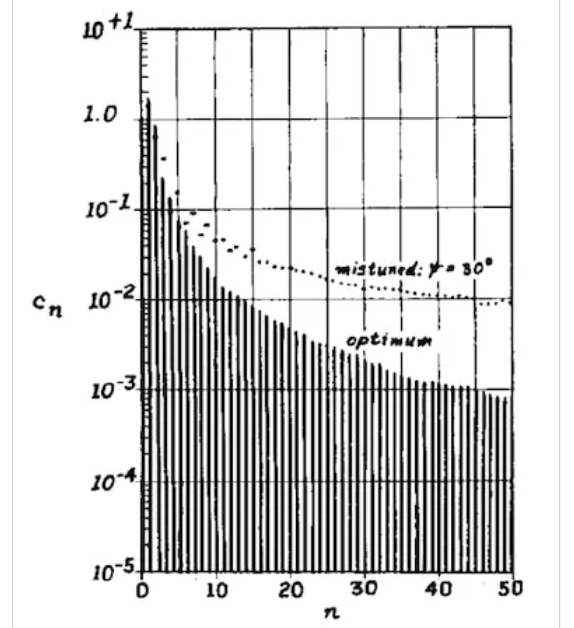
图3 E类驱动开关两端的电压频谱。图片由F.Raab提供
在最佳的E类放大器中,谐波分量的振幅随1/n2的减小而减小。表1给出了前五个谐波分量的振幅以及分贝增益。

表1 最佳E类放大器前五个谐波电压分量的振幅。数据由N.O.Sokal提供
顺便说一句,失调放大器的谐波分量以1/n的较慢速率减少。这在图3中用虚线表示。
负载电流频率内容
为了获得第n次谐波电流,我们将相应谐波电压(cn)的振幅除以该频率下负载网络的输入阻抗(Zn):
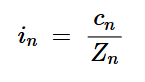
方程式2
基于上述方程,归一化为基波电流的第n次谐波电流的幅度为:
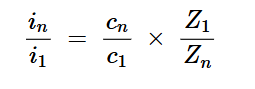
方程式3
负载网络在给定谐波频率下的输入阻抗可以通过串联谐振电路在该频率下的电抗来近似。对于图1中的放大器,这对应于L0和C0的串联组合。因此,我们有:
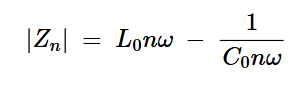
方程式4
在最佳E类放大器中,L0和C0的值由下式给出:
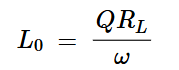
方程式5
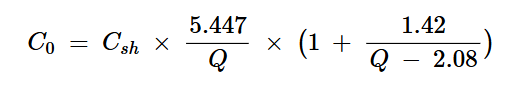
方程式6
其中RL是负载电阻,Csh是分流电容。为了找到Csh,我们使用以下方程式:
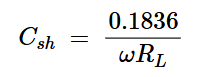
方程式7
将方程5、6和7代入方程4,得到归一化谐波阻抗Z1/Zn的表达式:
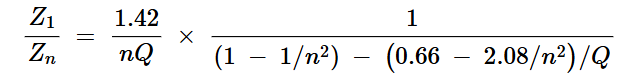
方程式8
在这个方程中,Z1/Zn仅是谐波数(n)和Q因子的函数。该方程表明,至少当n和Q相对较大时,Zn大致与n成比例增加。有关方程4至8的更详细讨论,请参阅n.O.Sokal和F.Raab的论文“E类射频功率放大器的谐波输出和负载耦合网络设计”。
接下来,表2显示了Q因子为5的前五个谐波频率的Z1/Zn比。

表2 Q=5时的前五个归一化谐波阻抗
将表1和表2中的值代入方程3,我们得到负载电流的谐波分量(表3)。

表3 Q=5时流入负载的谐波电流
对于Q=5的最佳E类放大器,负载电流的二次谐波和三次谐波分别比基波分量低19.85 dB和35.92 dB。无线电发射机的可接受谐波水平将在载波信号以下60dB的范围内。为了达到这些水平,我们需要在加载之前实现额外的过滤。如图4所示。
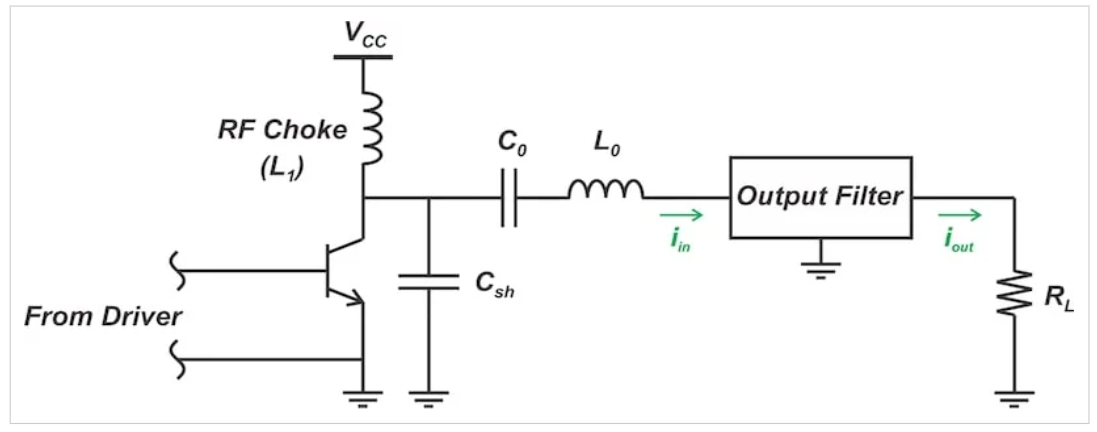
图4 带有附加滤波器的E类放大器。图片由Steve Arar提供
但是额外过滤了多少?在下一节中,我们将确定滤波器必须提供多少衰减才能将谐波抑制到可接受的水平。
确定所需的筛选器响应
我们的目标是使负载电流(iout)的所有谐波分量比基波分量低至少60 dB。从分贝转换,这意味着负载处的谐波分量应比基波分量低至少1000倍。
让我们从二次谐波开始。表3显示,在滤波器的输入端,二次谐波比基波低0.1017倍:
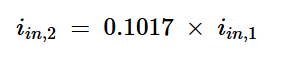
方程式9
其中iin,2和iin,1分别表示流入滤波器的电流的二次谐波和基波。
在滤波器的输出端,我们希望二次电流谐波至少比基波电流低1000倍:
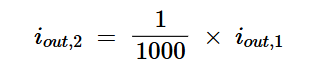
方程式10
为了将谐波分量抑制到所需水平,滤波器应在二次谐波处提供比一次谐波更多的衰减。如果滤波器在二次谐波处的电流增益相对于其在基频处的增益为A2,则我们应该得到:
方程式11
我们也可以用分贝进行这些计算。在滤波器的输入端,二次谐波比基波低|20log(0.1017)|=19.85dB。在输出端,二次谐波必须比基波低60dB。因此,二次谐波处的滤波器衰减必须比基频处的衰减至少大40.15dB。从线性角度来看,-40.15 dB对应于0.0098的衰减系数,这与方程11一致。
我们可以使用类似的程序来找到其他谐波频率下所需的衰减。为此,我们使用表3中的电流比率(in/i1)的分贝值。表4中显示了这些值以及滤波器电流增益(An)。

表4 所需的滤波器衰减,以使输出谐波在Q=5时比基波低60dB
请注意,对于高次谐波,所需的滤波器衰减较低。这是因为当我们向更高的频率移动时,E类配置的串联谐振电路呈现出更大的阻抗,因此衰减也更大。因此,外部滤波器所需的衰减较低。
总结
一个实用的E类放大器的Q因子可能在3到10之间。在这种情况下,我们需要在设计中加入一个输出滤波器,以防止过多的谐波电流流入负载。在本文中,我们确定了Q因子为5的设计所需的外部滤波。
请注意,谐波抑制并不是我们需要考虑的唯一要求。其他考虑因素,如阻抗匹配和带宽,可能会对滤波器设计提出额外要求。

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码