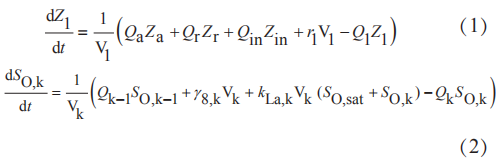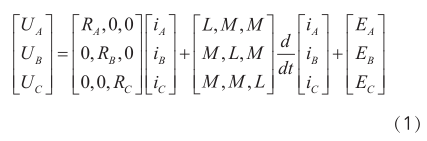电子产品世界

　　曾金芳，白冰，徐林涛(湘潭大学物理与光电工程学院，湖南 湘潭 411105)

　　摘 要：针对低信噪比下的环境声音识别效果不佳的情况，提出一种不同信噪比背景下的环境声音识别方法。

　　以伽玛通(Gammatone)变换的谱图为对象提取特征，生成灰度频谱图后映射成3种单色图，分别提取各单色图的扇形投影特征，在对得到的各方向的投影特征进行离散小波变换得到特征矩阵，并结合改进的最小均方误差(IMMSE)声音增强算法作为前端处理以减小噪声干扰，最后，利用支持向量机对带噪声音进行分类识别。实验结果表明：在-5dB的低噪背景下仍能取得较高识别率。

　　关键词：最小均方误差；声音识别；声音增强；谱图特征；扇形投影；支持向量机

　　*基金项目：湖南省自然科学基金（2018JJ3486）；湘潭大学校级科研项目(16XZX02)；湘潭大学博士启动基金项目(15QDZ28)

　　0 引言

　　声音信号与人类的生活密切相关，声音信号不受光线和视野影响并且需要的存储空间及处理难度低于视频信号，通过对环境声音信号进行识别可以获取丰富的信息，公共场所的声音事件识别可以有效地揭示该环境下的事件状况，可以弥补光线不足、受遮挡情况下的监控效果，声音识别技术广泛应用于安全监控、声音事件跟踪定位等领域，提取鲁棒性较好的声音特征 ^[1] ，有利于声音识别技术在现实环境中的适用性，所以背景噪声下的声音识别研究具有较高的实用价值。

　　在声音识别过程中，提取合适的特征向量对识别效果起关键的作用，声音识别的大多数的特征提取方法来源于语音识别 ^[2] ，常用的提取方法有Mel频率倒谱参数(MFCC)、短时能量、线性预测倒谱系数(LPCC) ^[3]等。近期的环境声音识别的研究主要有利用匹配追踪（MP）算法获得有效的时频特征，在MFCC特征的基础上利用原子字典进行特征选择，产生灵活、直观的特征向量然后用支持向量机(SVM)进行分类识别 ^[4] 。以上方法虽然简单有效，但真实的环境中存在各种背景噪声导致其识别效果明显变差。Dennis等提出子带功率分布(SPD)的特征提取来进行声音事件分类 ^[5] ，在声谱图的基础上提出子带能量分布对声音事件和噪声进行区分，利用图像处理的方法进行伪着色处理提取谱图的中心矩特征 ^[5] ，该方法在背景噪声下的识别具有一定有效性但在信噪比较低的情况下的识别效果有待提高。

　　现实环境中普遍存在着各种背景噪声，在前端处理中采用声音增强算法能改善识别效果，本文提出声谱图的扇形投影特征(Spectrogram Fan projection，SFP)算法。首先将环境声音信号转化为声谱图，然后将得到的声谱图进行扇形投影变换，得到各方向的投影系数组成特征向量，最后利用SVM分类器对特征向量进行分类识别。对于带噪声信号，提出改进的最小均方误差估计(IMMSE)算法作为前端处理来达到声信号的去噪效果。

　　1 声音增强算法

　　1.1 改进的logM M SE算法

　　考虑到环境声音噪声是非平稳的，传统的对数谱最小均方误差(Log-spectral AmplitudeMMSE,LSA-MMSE)能有针对性的减小噪声，其关键在于能否准确地估计先验信噪比， 本文采用改进的最小递归平均算法来估计噪声方差，结合logMMSE来达到声音增强效果，实验证明该方法对声音增强和消除“音乐噪声”有较好的效果。

　　建立加性噪声模型，设带噪声信号为：

　　式中，y(n)表示带噪声信号； x(n) 表示无噪声信号；d(n) 表示噪声信号；该算法从带噪声信号 y(n) 中估计出无噪声信号 x(n) 。纯净信号经短时傅里叶变换得到第k个频谱分量：Ak和Y(k) 。

　　由文献[6]中信号的估计可表示为带噪信号与增益函数的乘积：

　　式中， λx(k) 、 λd(k) 分别表示无噪信号和噪声信号的第k个频谱分量的方差； ξ k 、 γ k 分别表示先验信噪比和后验信噪比，先验信噪比是第k个频谱分量的实际信噪比，后验信噪比是加入噪声后第k个频谱分量所测得的信噪比。

　　1.2 IM M SE算法的实现

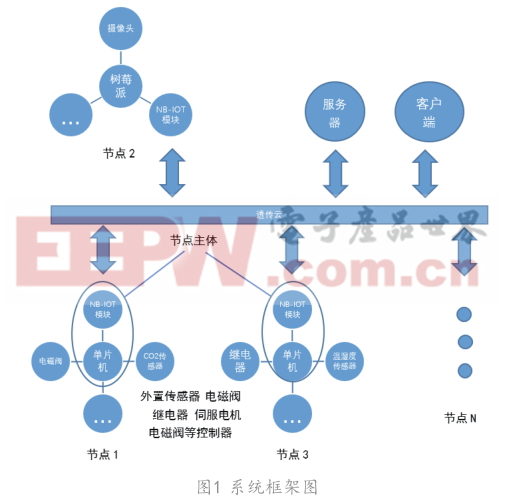
　　本文利用改进的最小值约束的递归平均（IMCRA）算法估计噪声方差。该算法利用平滑参数对噪声方差进行连续估计，平滑参数是时变参数，该算法是声信号中声音存在的概率的递归平均算法。声音不存在： H ₀^k 和声音存在：H ₁^k 的噪声估计表示为：

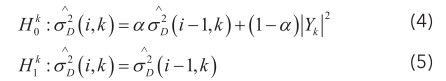
　　式中，i、k分别表示帧数和频点数，根据递归算法的通用形式 ^[7] ，可将噪声估计表示为：

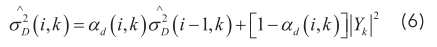
　　式(6)中的噪声估计表示为前一帧的噪声估计与当前带噪频谱的加权平均，式中， αd(i,k)=α+(1-α)p^(i,k)，表示时频相关的平滑因子，利用存在声音的条件概率 p∧( i,k ) 来计算平滑因子， 存在声音的条件概率p(i,k) 利用声信号功率谱与其局部最小值之比S_r (i,k) 作为阈值判断，根据递归算法的通用形式同理可得声信号的递归功率谱S(i ,k) 如下：

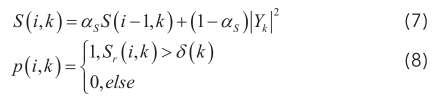
　　声音存在概率的估计利用时域平滑递归求得：

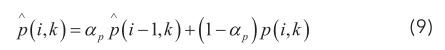
　　因为所取声音样本频率分布范围较广，故采用多阈值函数 δ ( k ) 采用频率相关函数来表示：

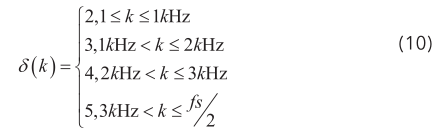
　　式中，fs为采样频率。结合公式所求得平滑因子α _d ( i,k ) ，利用式(6)，即可更新噪声功率谱估计，得到更新的噪声功率谱估计后，利用式(3)可求得增益函数，以此估计纯净声信号。

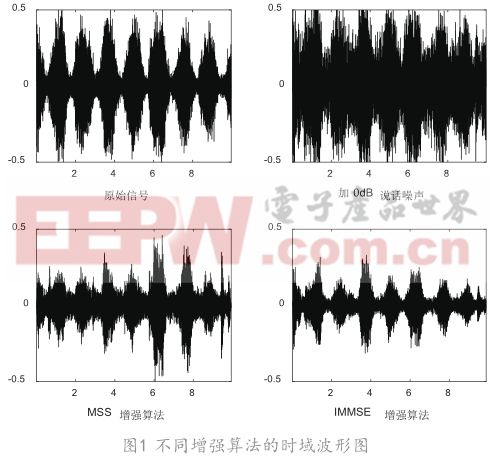
　　将 提 出 的 I M M S E 增 强 算 法 与 多 频 带 谱 减 法(Multiband Spectral Subtraction,MSS)对比，各增强算法的时域波形图如图1所示。其中横纵坐标分别表示信号采样点数和幅值。图1可了解IMMSE算法去噪效果较好。

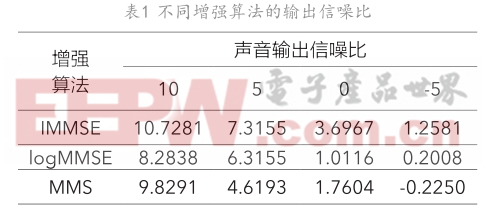
　　为进一步检验不同增强算法的去噪效果，对各增强算法检测其输出信噪比，根据检测带噪声音信号的指标定义：

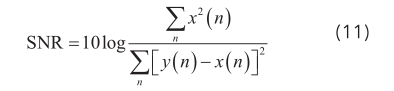
　　式中，计算出SNR的值越大，表示声音的质量越高，去噪效果越好，各增强算法的输出信噪比如表1所示。

　　2 特征提取

　　2.1 提取子带能量谱图

　　声谱图相比于传统的时域特征能表征更加丰富的声音信息，采用声谱图作为特征能同时分析声音的时域和频域特征，本文采用SPD谱图并对其进行增强改进，使声音的功率谱分布更明显。采用 Gammatone滤波器组生成的声谱图作为时频分析。参数设置为：100组中心频率为50 Hz到fs/2 Hz。将SPD归一化到对数域，表达式为：

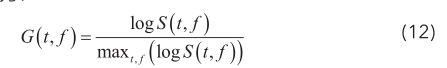
　　对数域的功率谱压缩了谱图的动态范围，以增强SPD中的频谱功率较高的像素点。谱图G(t,f)中像素点值的范围是固定的，SPD可表示为：

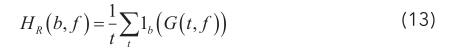
　　式中，b表示频谱功率；f表示频率；t表示样本的时间；实验中取b的值为100，1 _b 表示指示函数，基于“键盘敲击声”的SPD如图2所示。

　　2.2 扇形投影特征

　　扇形投影 ^[7] 特用于检测物体图像内部构造，计算图像沿指定方向由一点发出点光束，发散成一个扇形区域的投影变换，投影变换是图像沿x-y平面中指定方向的线积分。谱图H(b,f)的扇形投影变换的原理如下：

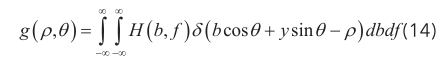
　　式中，g (ρ,θ) 表示经过扇形投影变换后重构的图像。

　　对每个声音样本的谱图H(b,f)进行扇形投影变换，角度 α 表示扇形投影的旋转角度，取值范围为[0,360]，规定旋转角度从x轴按逆时针的方向旋转每个角度的投影能将图像转换成一维的投影系数，图像各方向的投影系数组成的特征矩阵保留了图像的信息的同时降低了图像的参数大小，能够提高识别效率。

　　3 实验设计与结果分析

　　3.1 声音数据集

　　实验采用16类环境声音(键盘打字声、脚步声、锯子声等)，为确保实验数据的独立性，同类声音取自不同声音片段，一类包括20个样本，总共320个样本，具有较高信噪比，实验将其作为纯净声音样本，声音样本均来自于Freesound ^[16] 声音数据库，样本采样率为44.1kHz，量化精度为16 bit，单个样本长度2~3 s。实验中，随机选取每类样本的一半作为训练样本，另一半作为测试样本，按照信噪比20 dB、10 dB、0 dB、-5 dB作为测试。

　　3.2 实验参数

　　声音样本的预处理环节，对各声音样本分帧加窗处理，取帧长20 ms、帧移10 ms、窗函数采用汉明窗。

　　1)本文提出的SFP算法，扇形投影的旋转角度，在[0，360]中以15°为步长，取24个方向的投影变换。

　　2) MFCC算法，采用32组Mel滤波器组，每一帧提取13个倒谱系数构成MFCC特征。

　　3)对于SPD ^[5] 算法，采用64组Gammatone滤波器，提取2、3阶中心矩。

　　4)正交匹配追踪(OMP) ^[7] 算法，对声音信号进行稀疏重构，信号重构后提取MFCC特征，组成OMP的复合特征。

　　5)采用支持向量机(SVM)作为分类器，采用多分类的方式建立分类器。

　　3.3 实验结果与分析

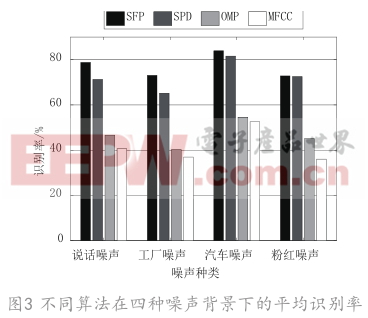
　　将SFP与SPD、MFCC、OMP、几种常用的声音识别算法进行实验对比。4种声音识别算法在不同噪声背景下的识别率如表2所示。纯净背景下，识别率如表3所示。本文的SFP算法在4种噪声下有较高识别率，特别是信噪比为-5 dB和0 dB的低噪条件下，在-5 dB的噪声情况下，最高比SPD算法高17.51%，平均识别率最高高出7.9%，比OMP和MFCC高出27.63%以上，平均识别率如图3所示。虽然文章算法在信噪比较高条件下的提升较少，但在低信噪比下相比其他算法能取得较高识别率。

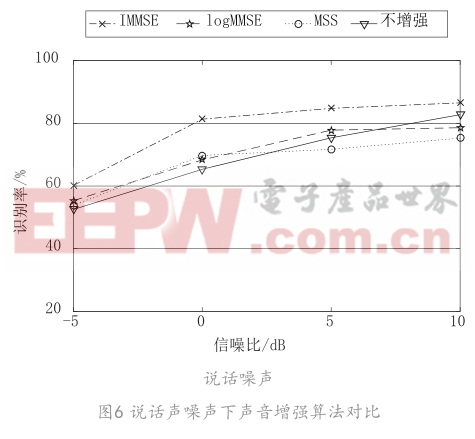
　　将提出的IMMSE增强算法与其他常用的声音增强算法进行比较，在4种不同的背景噪声的低噪条件下，信噪比分别取-5 dB、0 dB、5 dB、10 dB。

　　如图6所示为0dB的说话噪声背景下不同声音增强算法识别率。噪声条件下，本文的IMMSE的识别率高于其他增强算法，在-5dB和0 dB的低信噪比条件下不增强方法的识别率比增强后的识别率低，所以低信噪比条件下采用增强算法是可行的，说明SFP算法本身具有较好的抗噪性，实验证明SFP算法结合IMMSE增强算法在各种背景噪声下能取得较好的识别效果，适用于真实环境下的声音识别。

　　4 结论

　　针对真实环境的低噪条件下的声音识别，提出SFP算法，将谱图的扇形投影作为特征提取方法结合IMMSE声音增强算法，实验表明，在无背景噪声条件下，识别率达到96.72%；低噪条件下，平均识别率能达到73.05%；本文的方法噪声条件下具有较好鲁棒性，对比现有的SPD、OMP等算法，分类识别效果更好。

　　参考文献

　　[1] REN J, JIANG X, YUAN J, et al. Sound-EventClassification Using Robust Texture Features for RobotHearing[J].IEEE Transactions on Multimedia,2017, (99):1-1.

　　[2] BRADLOW A R, ALEXANDER J A. Semantic andphonetic enhancements for speech-in-noise recognition bynative and non-native listeners[J].Journal of the AcousticalSociety of America,2016,121(4):2339-49.

　　[3] JIAN-Chao Y U, ZHANG R L. Speaker recognitionmethod using MFCC and LPCC features[J].ComputerEngineering & Design,2009,30(5):1189-1191.

　　[4] CHU S, NARAYANAN S, KUO C CJ. Environmentalsound recognition with time-frequency audio features[M].

　　Institute of Electrical and Electronics Engineers Inc. The,2009.

　　[5] DENNIS J, TRAN H D, CHNG E S. ImageFeature Representation of the Subband PowerDistribution for Robust Sound Event Classification[J].IEEE Transactions on Audio Speech & LanguageProcessing,2012,21(2):367-377.

　　[6] SHIH J L, CHEN L H. Colour image retrieval based onprimitives of colour moments[J].IEE Proceedings-Vision,Image and Signal Processing,2002,149(6):370-376.

　　[7] NARASIMHADHAN A V, SHARMA A, MISTRY D. ImageReconstruction from Fan-Beam Projections without Back-Projection Weight in a 2-D Dynamic CT: Compensationof Time-Dependent Rotational, Uniform Scaling andTranslational Deformations[J].Open Journal of MedicalImaging, 2013, 3(4):136-143.

　　[8] SOUSSEN C, GRIBONVAL R, IDIER J, et al.JointK-Step Analysis of Orthogonal Matching Pursuit andOrthogonal Least Squares[J].IEEE Transactions onInformation Theory,2013,59(5):3158-3174.

　　本文来源于科技期刊《电子产品世界》2019年第9期第34页，欢迎您写论文时引用，并注明出处。

关键词： 201909 最小均方误差 声音识别 声音增强 谱图特征 扇形投影 支持向量机