定量测量多通道串行数据系统中的串扰引起的抖动(二)
对于这种串扰信号非常简单的码型,频谱是由一系列离散的峰值点组成的,使用两种方法都能够容易准确测量,因为所有的干扰源(Aggressor)抖动大于抖动噪声的门槛值。抖动的频谱如图10所示,随机抖动维持为一个常量,这和预期的是一致的,因为考虑到干扰源(Aggressor)和受干扰对象(Victim)之间的相位是恒定的。
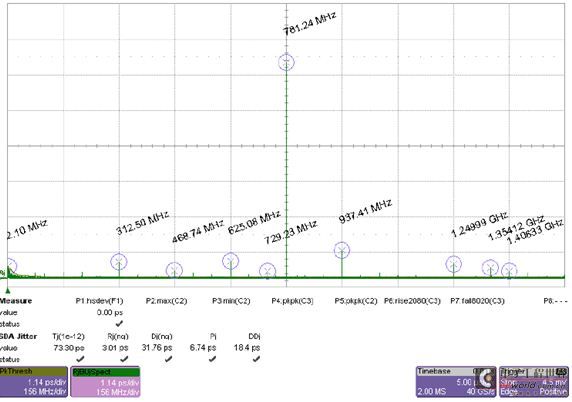
干扰源(Aggressor)和受干扰对象(Victim)之间有不同的相位关系时的随机抖动和固有抖动值测量结果如图11所示。
实验2 – 受干扰对象(Victim)为时钟码型,干扰源(Aggressor)为非重复性的数据码型
第二个实验利用随机的数据码型作为干扰源(Aggressor),以测量随机串扰的影响。这种串扰比简单的时钟码型对抖动的影响复杂得多,因为干扰源(Aggressor)的边沿转换是随机发生的,除此之外,上升时间和干扰源(Aggressor)与受干扰对象(Victim)之间的相位误差也是变化的。
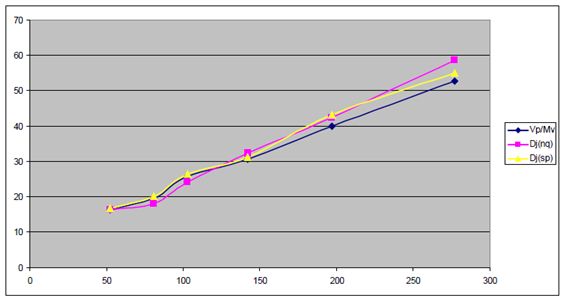
测量结果如表2和图12、13所示。NQ-Scale方法的随机抖动结果整体上要大一些,这是干扰源(Aggressor)的相位变化范围很大带来了受干扰对象(Victim)更小的上升时间所引起的必然结果。最显著的影响是当干扰源(Aggressor)的电平增加时,随机抖动增加,固有抖动减小。这和理论分析是一致的,因为干扰源(Aggressor)的抖动频谱由很多距离很近的线组成,而且由于频率分辨率有限,这些线看上去是连续的,可从图14清楚地看出来。图中显示的噪声基底具有和方波脉冲一致的形状。
根据等式3预测的抖动结果比NQ-Scale的都要大一些。为什么会这样? 等式1说明了串扰的大小和干扰源(Aggressor)的微分结果成正比。快沿比慢沿有更大的延迟,因此受干扰对象(Victim)和干扰源(Aggressor)之间的相位差更大。 因为相位误差越大,串扰引起的抖动的峰值就会越小,等式3的预测是基于串扰电压的峰峰得到的,因此结果总会偏大一些。
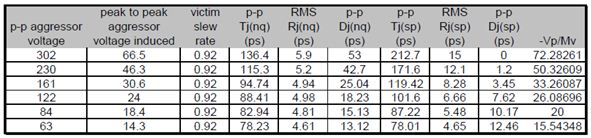
表2 干扰源(Aggressor)为非重复性的数据码型 的抖动结果
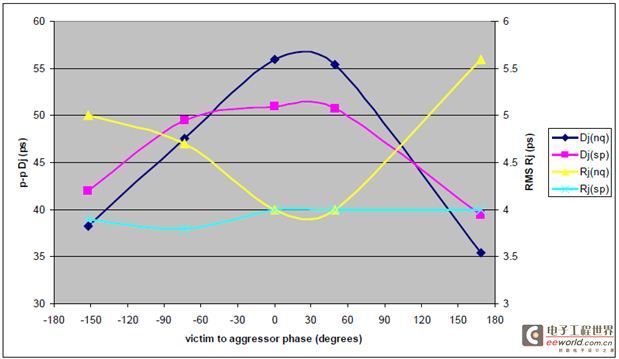
图13表示用频谱方法,NQ-Scale方法及理论预测的总体抖动。总体抖动的预测值是根据基线的随机抖动值4.61ps和根据等式3预测的固有抖动值计算得到的。 QN-Scale方法的测量结果和预测的结果非常一致,但是频谱方法测量出来的抖动值明显大很多,这是因为它不能从Rj中准确地分离出BUj。 固有抖动的减少和随机抖动的增加是非常吻合的。
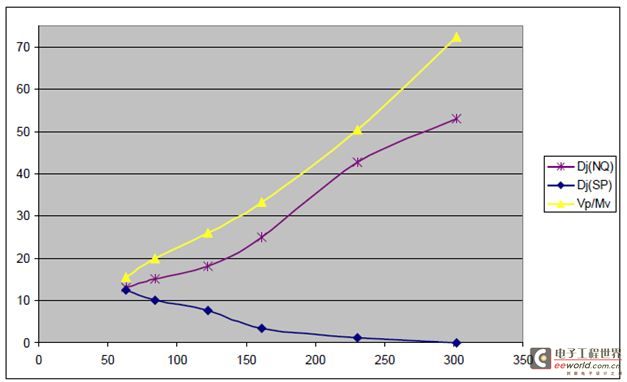
图12 固有抖动和串扰大小之间的关系 (干扰源(Aggressor)是随机数据码型)
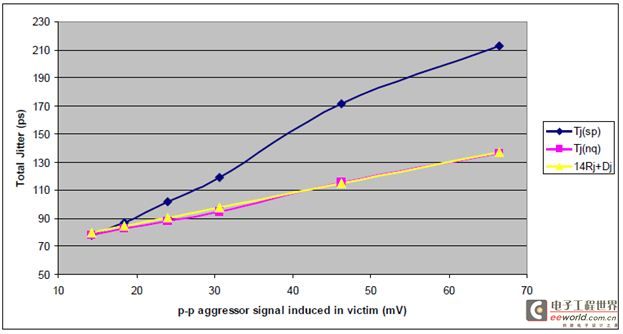
图13 总体抖动 VS. 干扰源(Aggressor)电压(受干扰对象(Victim)是时钟,干扰源(Aggressor)是非重复性的数据。
关键词: 定量测量串行数据系统串扰抖

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码