电子产品世界

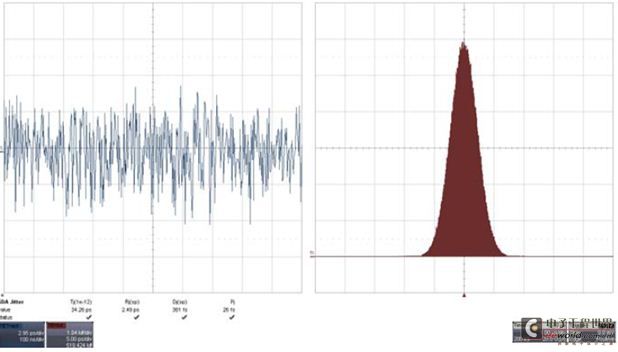
图2 抖动追踪（左）和直方图（右）

所谓的频谱分析方法被用于解决上述直接测量的局限性，该方法利用FFT将TIE的追踪图转换为频域，分析抖动的频谱得到抖动参数。这个方法的原理就是要把随机噪声的频谱从固有抖动中“甄别”出来。这种分离方法需要定义一个幅值门槛，低于该门槛的FFT定义为随机噪声，高于该门槛的则为固有抖动。固有抖动的特点是它的频响表现为离散的“峰值点”。通过将门槛值以下的FFT的Bins以平方和相加得到随机抖动，因为这个方法中将随机抖动都假设为随机的和不相关的。这种计算Rj的方法计算速度快，可重复性好，这两点对于测量来说都是很好的特点。Dj则可以通过多种方法得到，譬如拟合抖动的直方图或者对门槛值以上的FFT的bins做复杂的加法运算。

频谱方法是测量双狄拉克(Dual-Dirac)模型参数的初级方法，事实上也是非常有效的方法。但是频谱方法的一个先天性的不足是它是建立在这样一个假设前提下的：所有的随机抖动都是高斯分布的。通常来说实际中当然没有真正的高斯但是至少大多数的随机行为在实际的测量时间范围内是非常接近高斯分布的。但是也有些伪随机的案例，在短时间内表现为随机的，而实际上在比较长时间内观察则是属于固有抖动。还有些情况下虽然是随机抖动，但是其分布特性并不是高斯的。在这些情况下，频谱方法的假设就不成立了，Rj就会比实际的大或者小。

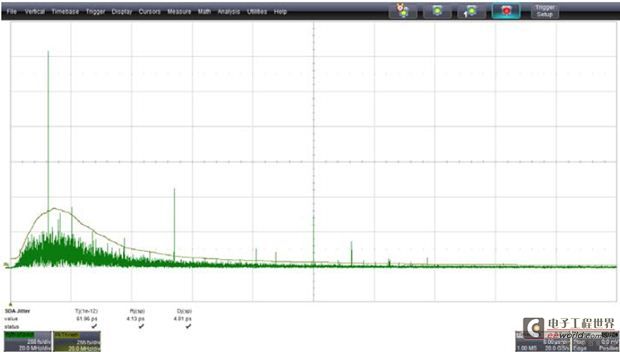
图3 带有门槛的抖动频谱图。低于门槛幅值的Bins被定义为随机噪声

频谱方法遇到的另外一个问题是随机抖动的分布并不是单一的高斯分布，而是由多个高斯分布组成。例如，对于一个特定信号的每一个边沿可能是由一个在它之前的边沿引起的独特的上升时间。这在传输通道带宽受到限制而造成了ISI的情况下是很常见的。除了造成有些比特位的幅值减小，ISI还使一些边沿的转换速率降低。 更低的转换速率带来信号中更多的噪声，这些噪声会转换为时序上的抖动。 根据数据码型的不同，边沿上很小的变化可能会有更高的随机抖动，结果表现为在抖动分布上有一个主体的高斯抖布和一个很小的、低统计权重的高斯。如果这种低权重的高斯有一个比较高的标准偏差值，那么正确的方法应将此作为随机抖动值，但是，频谱方法仅仅是计算出了低分布，高权重的高斯，测量到的Rj就会偏小。

串扰带来的抖动行为就属于频谱方法不能准确测量的类型。有些情况下，串扰带来伪随机抖动，这时的干扰源(Aggressor)和受干扰对象(Victim)是不相关的。在另外一些情况下，干扰源(Aggressor)是和受干扰对象(Victim)相关的，但是这时候的码型一般特别长而且不重复的。 在这些情况下，抖动是伪随机但是有界，导致频谱方法会过高估计了抖动大小。

抖动分解

双狄拉克(Dual-Dirac)模型对于评估串行数据链路长时间的误码性能是有效的，但是仅仅从Dj参数来确定固有抖动的根源是不够的。抖动测量仪器对固有抖动的组成成分进行更详细的分析以找出抖动的根源。图4是一种典型的抖动分解树，固有抖动包括数据相关性抖动DDj和非相关性抖动。数据相关性抖动DDj通常是由背板、电缆和连接器等组成的信道衰减和散射等引起的，而非相关性抖动则是从外部源如开关电源和串扰耦合到信号中的。

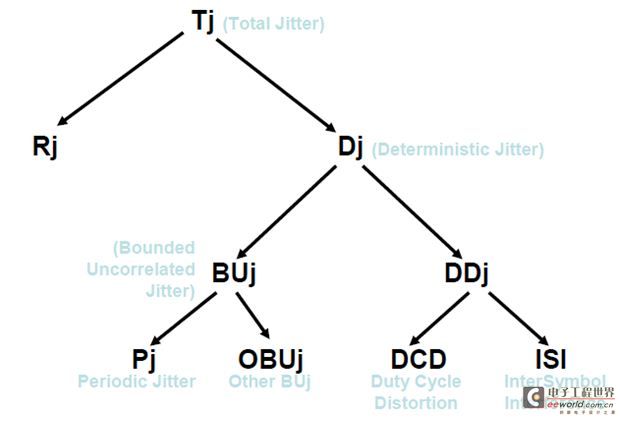
图4 抖动分解树

非相关性抖动常被称做有界的非相关性抖动（BUj）。这种抖动通常可以根据频谱中的频率成分测量，它的分布是有界的，也就是说BUj的峰峰值范围是限定在一定范围以内，不会象高斯抖动那样随着观察时间的增加而增加。有些有界抖动并没有表现出离散的频率成分，至少在测量到的时间范围内它的表现形式是随机的。这种抖动被定义为其它的有界不相关抖动（OBUj）。应该注意到一些抖动模型将Pj单独作为一种类型而不是当作BUj的一部分，但是MJSQ[1]中将Pj当作BUj的一部分。不管BUj是否包括Pj，这并不影响抖动的整体分解结果，因为这只是一个词意上的分歧。两种情况下，Pj都是和数据码型不相关的。

关键词： 定量测量串行数据系统串扰抖