一类可变参数数字均衡器的设计
对二阶可调均衡器,设K=3.5,α=0.8,β变化时和设K=3.5,β=0.4,α变化时的频响特性曲线如图8和图9所示。
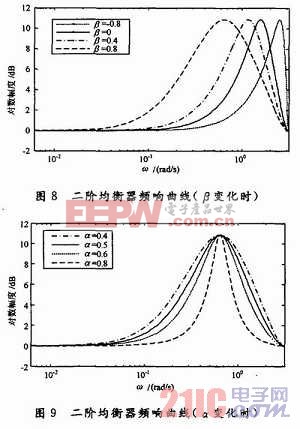
与一阶均衡器相比,二阶均衡器有一个谐振峰,在它的可变参数中,谐振峰的位置取决于β,幅度取决于K,而它的带宽取决于α。实际的音乐播放器中均衡器可以采用由多个调谐在不同频率上的二阶均衡器级联组成。
3 均衡器均衡实例分析
利用计算机上的硬件和Windows操作系统,结合Matlab软件,可以很方便地进行音乐信号的采集、变换、存储、分析、处理和重构。本文利用Windows自带的录音机录制了一段音乐信号,它的采样频率为22.050 kHz,保存为test.wav文件。利用Matlab软件的命令wavread将音乐文件读入变量x,作为均衡处理的信号源,[x,Fs,N bits]=wavread(‘text.wav’)。
然后对转换后的音乐信号利用Matlab的命令FFT作快速傅里叶变换,X=FFT(x),得出音乐信号的波形图和频谱图如图10所示。
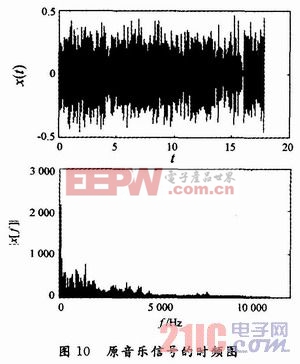
3.1 一阶低频均衡处理后的结果图
设定一阶低频均衡器的参数K=2.5,α=0.4和K=2.5,α=0.8对处理后的音乐信号时域用Y(t)表示,频域用Y(f)表示。源音乐信号做均衡处理,处理后的结果如图11所示。
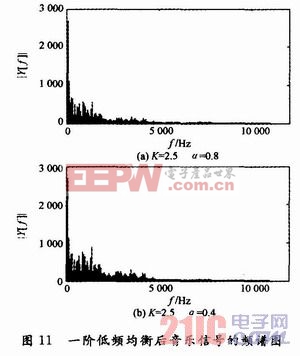
由图11可知,均衡后低频部分的幅度都有所增大,由K控制,α=0.8时,均衡的频率范围大约是0~2 000 Hz,而α=0.4时均衡的频率范围大约为0~4 000 Hz,由此可知,参数α的变化控制均衡的带宽范围,α越大,均衡器截止频率越小。试听均衡后的信号,音量变大,低频部分增加,音乐变得厚重、雄浑,二者音色均发生变化。

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码