基于RSSI测距和距离几何约束的节点定位算法
Cayley-Menger行列式及距离几何约束
距离几何理论中,Cayley-Menger行列式可以被用来处理不变空间的欧拉距离几何问题[6,7]。两个n点序列{ P1,…,Pn }和{ q1,…,qn }∈ Rm组成Cayley-Menger矩阵,且定义为:
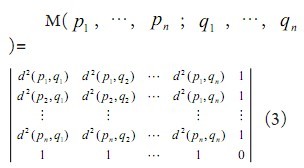
其中,(i,j {1, …,n}为pi点和qj之间的欧式距离。两个n点序列的Cayley-Menger行列式定义为:
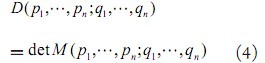
当两个序列相同时![]()
![]() ,
, ![]() 被称为Cayley-Menger行列式。在RSSI测距过程中,由于多径、绕射、障碍物等因素,不可避免出现测距误差,设未知节点与锚节点之间的真实距离与测量距离。设未知节点接收到锚节点 的测量信息,根据节点集合
被称为Cayley-Menger行列式。在RSSI测距过程中,由于多径、绕射、障碍物等因素,不可避免出现测距误差,设未知节点与锚节点之间的真实距离与测量距离。设未知节点接收到锚节点 的测量信息,根据节点集合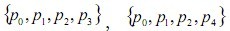 ,…,
,…,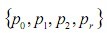 结合[3]利用Cayley-Menger行列式的经典理论的推导,可得到r-2个独立的二次距离约束等式,
结合[3]利用Cayley-Menger行列式的经典理论的推导,可得到r-2个独立的二次距离约束等式,![]() 。
。 ![]() 作为未知节点与锚节点在测量过程中出现的误差,在距离约束限制下形成平方误差最小化非线性问题:
作为未知节点与锚节点在测量过程中出现的误差,在距离约束限制下形成平方误差最小化非线性问题:
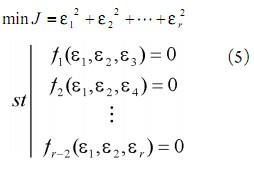
运用数值分析方法,求得最优解 ![]() ,进而得到未知节点与锚节点位置估计值:
,进而得到未知节点与锚节点位置估计值:
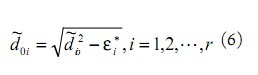
三角形质心定位算法模型
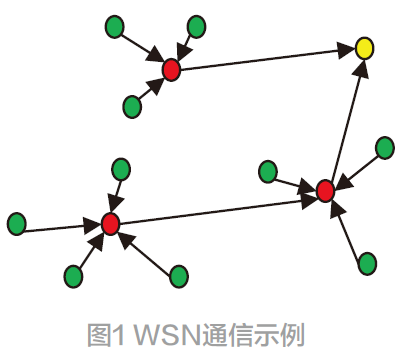
本文研究了未知节点与其无线射程范围内的三个锚节点之间的通信约束和几何关系得出了未知节点所在三角区域,将三角形的质心作为未知节点的估计位置[8,9] 。这里的三角形质心定位算法的基本思想是:三个锚节点A、B、C,未知节点D,利用RSSI和距离几何约束算出节点A和D的距离为;节点B和D的距离为;节点C和D的距离为。分别以A、B、C为圆心rA,rB,rC , 为半径画圆,可得锚圆交叠区域,通过计算三个锚圆交叠区域的三个特征点的坐标,以这三个点为三角形的顶点,未知点即为三角形的质心(如图1所示)。
假设已知3个锚节点的坐标分别为A(Xa,Ya) 、B(Xb,Yb) 、C(Xc,Yc) ,与未知节点的距离分别为rA,rB,rC ,通过下面的公式求出。
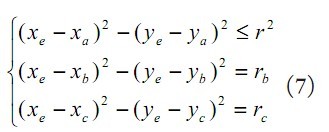

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码